更多
分享

仔細打量一下: 6174。
乍看沒什麼奇特之處,但是,自從1949年以來,它一直令數學家、數字控抓狂、癡迷。
為什麼?接著往下讀。
輪到 8352
現在的數字是 6174,用這個數字再算一遍。從大到小減去從小到大:
到了6174,就沒有必要繼續下去了,因為結果總是一樣的:6174。
你以為這是巧合嗎?隨便再挑一個數試試,比如:2005。
還是信了吧。不管你挑的四位數是什麼,早早晚晚你都會遇到6174;而且,遇到6174就只能止步,否則面臨的將是無休無止的無用功了。
也許你還喜歡:

祝賀一下,現在你總算搞懂了卡普雷卡爾常數(Kaprekar's constant,又稱卡布列克常數)。
印度數學家卡普雷卡爾(1905-1986)最喜歡擺弄數字,正是他發現了6174的神奇魅力。
自認數字理論控的卡普雷卡爾1949年在印度城市馬德拉斯召開的一次數學會議上向世界宣佈了自己的發現。
他常說的一句話是:「醉漢一定會接著喝酒,因為他希望快感持續下去,我和數字的關係大同小異。」
卡普雷卡爾就讀於孟買大學,畢業後在孟買北部山區小鎮帶奧拉利(Devlali)當老師。
印度數學家認為,卡普雷卡爾的發現很無聊,取笑一番,置之不理。不過,卡普雷卡爾是位高產作家,經常在大眾科普刊物上發表文章。而且,他還常被請去參加各種會議、在學校巡迴演說,介紹自己獨特的方法和有趣的發現。
逐漸,卡普雷卡爾在國內外知名度、受歡迎程度越來越高。到了1970年,美國暢銷書作家、數學愛好者Martin Gardner在著名科普雜誌《科學美國人》上發表文章介紹卡普雷卡爾。
現在,卡普雷卡爾的名字在全世界數學愛好者——特別是數字控中——已經是如雷貫耳。
日本大阪經濟大學教授西山豊(Yutaka Nishiyama)認為,6174真是個「謎一樣的數字」。在一篇網上文章中,西山教授解釋說,他用電腦查證是否所有的四位數都能在有限步驟內得出6174。
他的發現是,根據卡普雷卡爾的算法,所有四位數(只要四位數不重覆)最多只需要7步運算就會得出6174。
「如果7步還沒有得出6174,那一定是你算錯了。重來一遍吧。」
也許你會想了,除了6174,還有沒有其他什麼魔數呢?答案:我們不能肯定。但是,我們已經知道的是,3位數當中也存在類似的卡普雷卡爾現象。
試一試。隨便找一個3位數,比如說574。
好了,魔數找到了:495。
數學家說,這種常數值發生在3位和4位數中,但是,科學家試過的只是2位到10位數。

印度城市孟買南部的「Scigram技術基金會」為鄉村、偏遠地區學校開發「IT學習平台」,他們選定特殊的6174,試了試這個數字和顏色關係的有趣之處。
該公司的創始人告訴BBC,他希望證明數學同樣很有趣,以此鼓勵學齡兒童,特別是那些痛恨數學的孩子。
「卡普雷卡爾常數真的很美。按著步驟一步步做,你總會遇到『啊』那個精彩的瞬間。按著傳統的數學大綱學數學,一般碰不上這樣好玩的事。」
Scigram團隊給得出6174這個常數的不同運算步驟編上顏色碼。記住,最多只要7步。
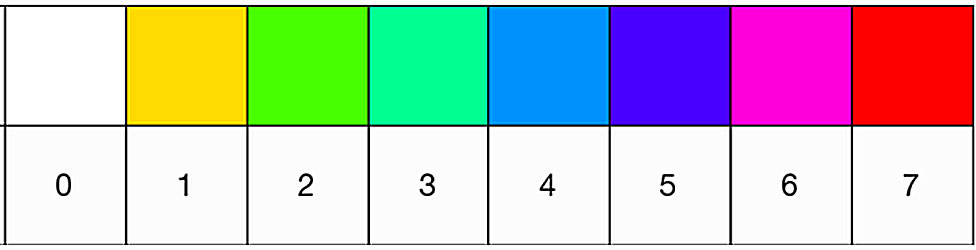
然後,用學校中常用的樹莓派(Raspberry Pi)廉價電腦、Wolfram編程語言解讀已有的一萬個四位數得出6174常數所用步數,排列在彩色網格上。
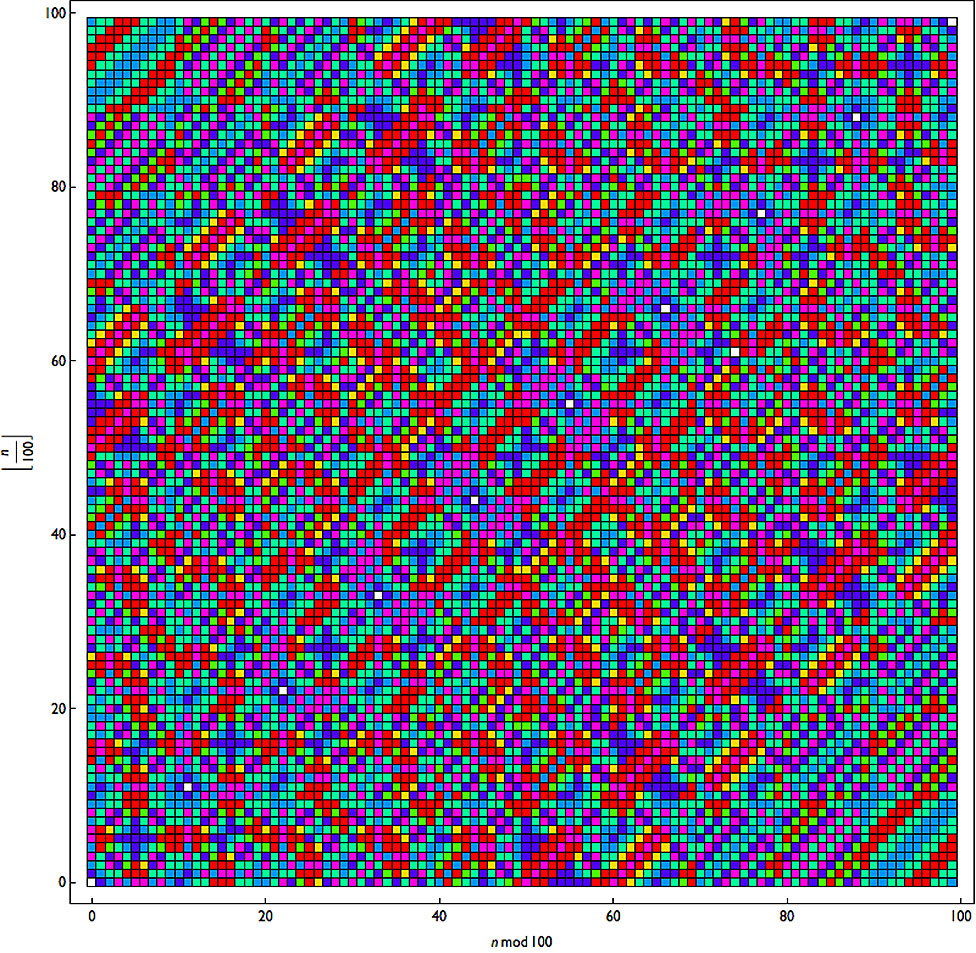
如果藍色代表奇數、綠色代表偶數,結果是什麼樣?
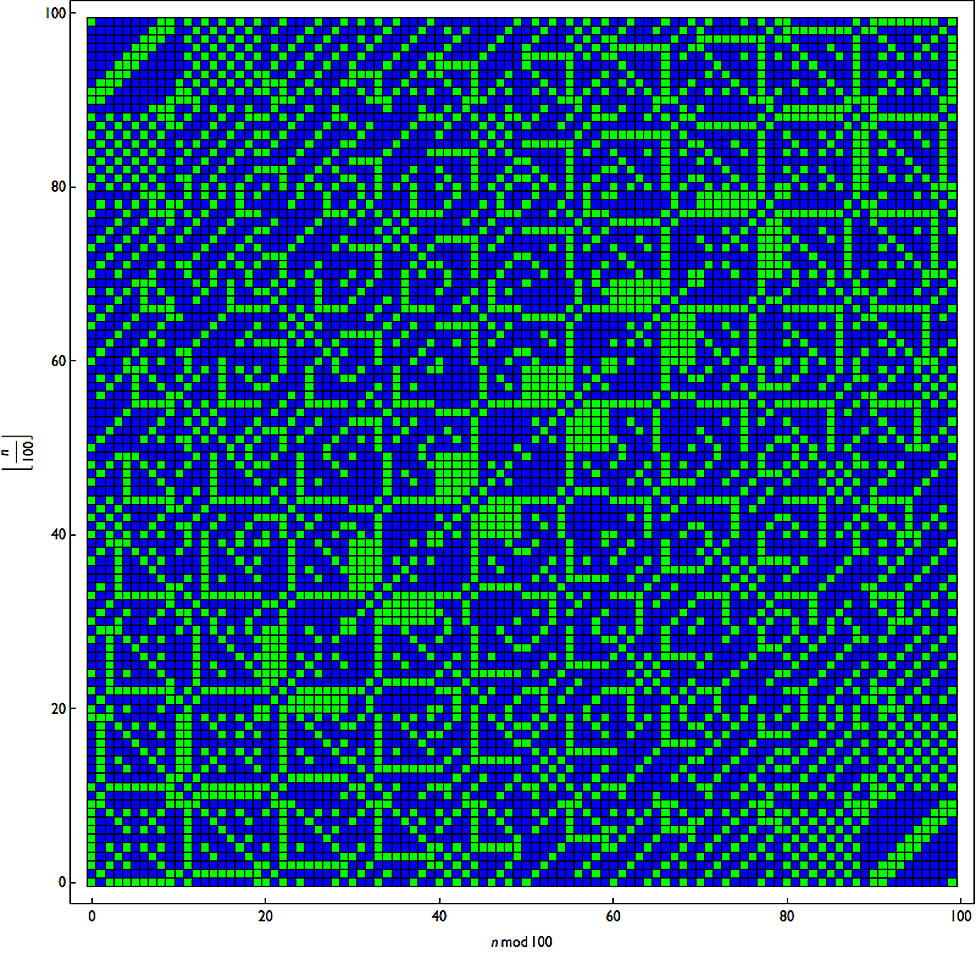
如果用綠色代表質數,藍色代表其它數字,變化大嗎?
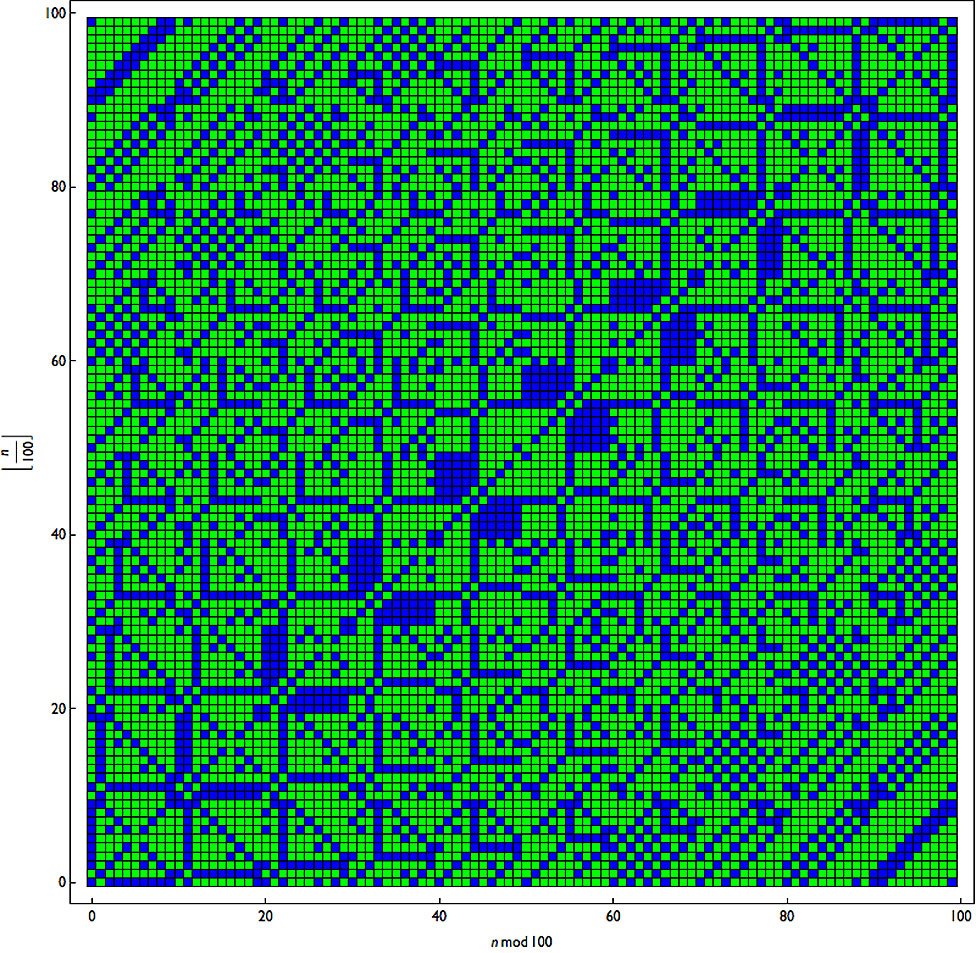
6174常數並不是卡普雷卡爾的唯一貢獻。你有沒有聽說過卡普雷卡爾數(卡布列克數)?它指的是具有以下性質的數:
它的平方可以分成兩個正數,兩數之和等於原始數字。舉個例子可能更加一目了然:
其它還有: 9, 45, 55, 99, 703, 999, 2,223, 17,344, 538,461......
找幾個自己試一試吧。記住,分平方值的時候,只要可能必須位數等分,比如,一位加一位,二位加二位。
但是,如果平方值的位數不能等分,比如上面這個例子88209,它是五位數,那就只能分成兩位數88和三位數209了。
順便說一句,做的時候不要忘了,這叫做卡普雷卡爾運算。
看,你同樣也可以成為娛樂數學大師!
