更多
分享

見過海王星(Neptune)嗎?它是太陽系的九大行星之一,距離地球43億公里,站在地球上仰望,它就是夜空中一個白點,遠不如離地球較近的水星、火星那麼晶亮、耀眼。
海王星的發現很大程度上歸功於數學 - 科學家先算出它的可能方位,然後才用天文望遠鏡找到它。
這個發現被載入科學史冊,被賦予的意義中有一條:這是一個證據,證明了數學並非人類的發明創造,而是客觀存在。

牛頓的萬有引力理論在19世紀被用來計算太陽系行星繞太陽公轉的軌道,基本上沒什麼偏差,除了天王星。
天王星是那時已知行星中離太陽最遠的一顆;它的運行軌道似乎總是偏離根據萬有引力定律推算的結果。
當時有些學者猜測,也許萬有引力定律對如此遙遠的星球可能不適用。
另外有些科學家則求助於數學,通過計算,推測天王星附近存在一團體量巨大的物質,導致它繞日公轉軌道出現偏離。
倫敦大學學院天文物理學家魯西·格林(Lucie Green)解釋說,他們通過計算結果推測這團神秘物質可能在什麼方位,然後把望遠鏡盯住那個地方,結果就發現了這顆後來命名為海王星的第九大行星。

本來,天王星、海王星的故事到此可以告一段落。但編寫歷史的人把海王星跟數學這麼一關聯,問題就來了。
數學究竟是人們發明出來、用以表述現實物理時空的抽象模型呢,還是它本身就是一種現實存在?
聽起來像哲學問題,實際上也確實是哲學家千百年來一直在琢磨的問題。
而且,對這個問題即使到了今天仍沒有共識,意見分歧極深。

我們試著來啃一下這道千年難題。
數學始於人類生存活動的需要:計數和丈量。
以蛋糕為例。數學家們對蛋糕有各種說法:尺寸、重量、形狀、怎麼切割。所有這些都是具像、可見的。
數學還可以把我們帶到抽象的領域:如果你吃了三分之一的蛋糕,那麼剩下的就是三分之二,兩塊。把這兩塊吃了,就沒了。
數學家貝婁斯(Alex Bellos)說,古人用數字運算、丈量時,還沒有負數的概念。
如果現實意味著有形有體的物件,可以計數、量尺寸和重量,那麼比零更小的概念是很難想像的。
一隻蛋糕,吃完了就吃完了,沒有「負三分之一」塊蛋糕之說。

不過,在黑與白中間的灰色地帶,負數這個概念和自然,完全能夠被人理解的,那就是錢。
錢這個東西,你可以有,也可以欠。
負數最初的應用是從債務和記賬開始的。
你欠別人5塊錢,我給了你5塊讓你還給別人,你手裏剩下零。這就是負數現實的起源。
然後事情就一發不可收拾,到今天人們已經無法想像不存在負數的世界。
故事還沒完。上面這些都根植於現實世界,但負數似乎自帶魔力,能讓不可思議的事發生。
兩個負數相乘,得到的結果是正數,負負得正:(-1) X (-1) = 1。
就這麼簡單的一個定律,牽出了一個實實在在的、巨大的謎。
貝婁斯解釋說,如果在數學等式裏擺弄負數和正數,會看到奇妙的結果:
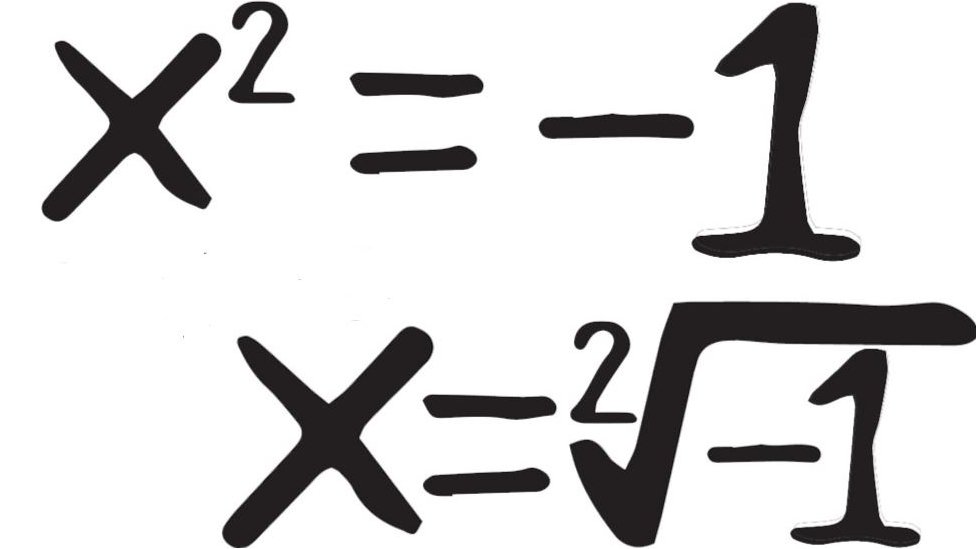
這是啥?一個數的平方,即一個數乘以自己,等於-1;那麼-1的平方根就是這個數,但這怎麼可能?
數學家貝婁斯說,這個數不可能是正數,也不可能是負數,因為負負得正。
於是,偶然發現這個謎的人們陷入困惑。這太荒誕了。
後來,數學家們逐漸開始意識到,這確實不尋常,但實際應用中卻能推導出正確答案。所以,這個謎就留給哲學家們去絞腦汁吧。我們數學家只要數字,只要答案。
這時,一扇從現實通向非現實的門悄悄打開了。
當然,全部扔給哲學家去解釋是不可能的;數學仍舊可以用來解釋這個現象。
-1的平方根有一個名字,叫做「虛數」(imaginary number)。
貝婁斯說,這個名字不是很好聽,因為數學本身是真實的,但「虛」卻給人不真實的印象。
但其實數學從一開始就是虛的,是抽象的。比如三塊蛋糕,我們看見的是蛋糕,而「三」則是個抽象概念。

虛數也一樣,看起來很荒誕,但仔細琢磨,就會發現它很符合邏輯。
貝婁斯解釋說,我們所說的實數,加上虛數,還有複數,共同構成了一種邏輯語言,能夠用來完美詮釋許多現象,比如循環旋轉。
他說:「今天,-1的平方根在我們看來就和-1一樣真實,即使它對於我們來說很難理解,就像-1這個數對我們的老祖宗來說無法理喻一樣。」
現在輪到複數(complex number) 。有些用實數無解的方程式,用複數就可以解答。
它們就是那麼魔性,對我們理解現實提供了實際幫助,幾乎所有涉及循環旋轉和波浪的數學題離不開複數這個工具。
複數在電機工程、雷達、醫療影像領域不可或缺,對解釋次原子粒子的行為也至關重要。
那麼問題又來了:為什麼只存在於數學假設中的東西,在現實世界用途如此之大呢?
匈牙利20世紀物理學家尤金·維格納(Eugene Wigner)認為這就是個奇蹟。還有不少人跟他看法一致。
維格納1960年發表了一篇重要論文,其中把複數叫做「數學在物理科學中不合理的有效性」(unreasonable effectiveness)。

如果數學是人類發明設計出來,用作表述現實的工具,那麼它具有這種功能難道不是合情合理,完全符合邏輯嗎?
有什麼「不合理」的呢?
這個問題或許要找數學、物理兩棲的專家來解釋,比如埃莉諾·諾克斯(Eleanor Knox);她的專業領域是物理中的哲學。
她說,確實,如果發明數學是為了幫助我們理解物理系統,那麼它勝任這個任務完全合乎邏輯。但數學的演變過程似乎跟這種解釋不相符。
歷史上不乏這樣的先例:數學家純粹出於個人興趣做出了一些發明, 過了段時間這些發明恰好用來促成某項重大的物理學發現或突破。
數學中的非歐幾何(non-Euclidean geometry)就是一個著名的例子。
在19世紀末的時候,許多數學家都迷上了非歐幾何,就因為他們覺得這個命題非常有意思,引人入勝。
當時公認整個世界都可以用歐幾里德幾何定律來表述,學校教的也是歐幾里德,比如三角形的三個內角之和是180度。
1800年代末期的數學家並不想推翻歐幾里德幾何學,只不過是在數學探索過程中發現了妙不可言的新的數學結構。

諾克斯說,到了20世紀,愛因斯坦在廣義相對論研究中發現自己需要一種新的理論用來表述相應的時空定律,而非歐幾何正好滿足了他的需求。換句話說,如果沒有非歐幾何,愛因斯坦的相對論就不會問世。
但是,19世紀沉浸在非歐幾何研究中的數學家很顯然沒有預見到多年後物理學界會出現廣義相對論。
諸如此類的史實難免令人產生各種聯想:數學和現實世界的關係如果不是奇蹟,至少稱得上令人驚詫。
現代物理學不斷發展,學問越來越精深,凡夫俗子如你我離其中蘊含的複雜的數學越來越遠,對數學所表示的古怪現實也越來越難以理解。
當然,這也不奇怪。沒有任何理由認為我們憑感官接觸到的日常現實就是宇宙現實之根本。
真正令人驚奇的是數學可以幫助我們在人類感官無法企及的時空展開探索。
接下來的問題是,在探索現實本質的過程中,數學的表述能力是不是有極限?
諾克斯說,20世紀誕生了兩個偉大的物理理論:量子力學和廣義相對論。
但是,這兩大理論背後的數學架構卻像一對老死不相往來的夙敵,要把兩者整合起來,其複雜程度難以複加。

諾克斯解釋:「沒有一個連貫、耦合的框架來幫助我們理解這兩大理論是如何在同一個世界並存的,它們是怎樣表述同一個現實本體的。」
這方面的探索難度之大常人無法想像,科學實踐中最基本的紐帶 - 思想和實驗之間的紐帶 - 在這裏似乎斷了。
這難道就是數學的極限嗎?
諾克斯認為,到目前為止,我們可以得出幾個結論:
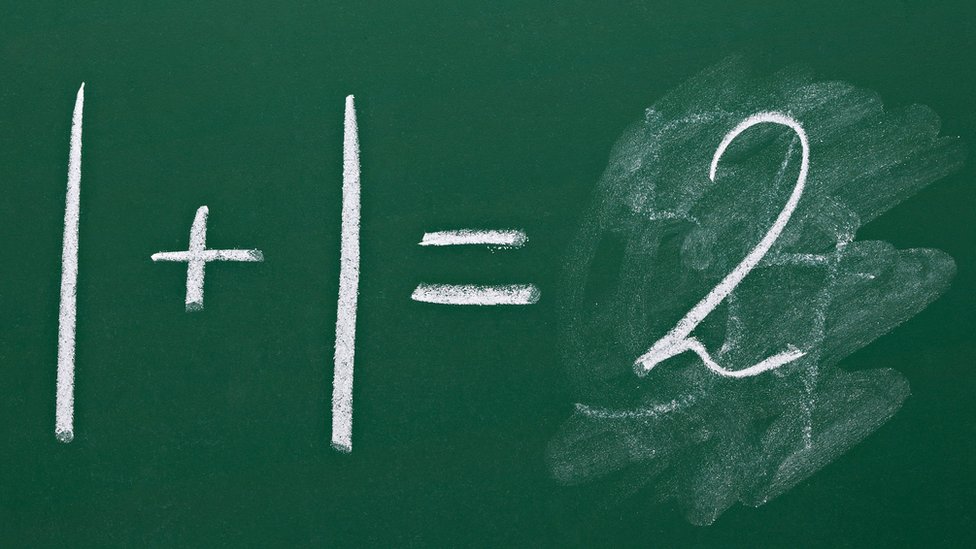
也許我們對自己太苛刻,或者太狂妄,想讓數學定律和物理定律手拉手步入同一個殿堂 - 這件事比登天還難,就因為它們是兩回事。
愛因斯坦曾經說過,數學定律離現實越近就越不確定;數學定律越確定,離現實就越遠。
諾克斯這麼解釋:數學有一個特點,非錯即對。我用數學來驗證一件事,誰都不會有疑問。但物理就不是這樣。
這正是數學和物理的最大區別之一。
物理定律和理論經常會錯。牛頓的萬有引力定律很美、很高雅,而且經常是有意義的,但它們不代表全部的真理。
諾克斯預言,毫無疑問,未來的科學家將能夠證明愛因斯坦的理論也只是「大致正確」。

數學從哪裏來?這個問題應該問數學家。
鄭樂雋(Eugenia Cheng)是芝加哥藝術學院駐校科學家,出生在英國,劍橋大學畢業。邏輯和藝術是她感興趣的話題之一。
她的專業是範疇論(Category Theory),也被稱為數學的數學,研究數學王國中各個不同領域之間如何建立聯繫,架橋鋪路。
她說:「我確實感覺自己是在發現概念,然後發明思考它們的方法。我做抽象研究時,就覺得自己像在抽象的叢林裏漫遊、探索,然後發明一種方式來談論它們,將它們理論化、系統化,這樣我就可以梳理自己的思想並與人交流。」
確實很難想像還有什麼比這更抽象的工作。
那麼,鄭樂雋研究過的那些數學家是不是跟現實有關聯呢?
「別人跟我提現實,我就想反問:到底什麼是真實?
我們稱之為『現實』的只不過是我們假設真實事物的幻像,因為我們大家都傾向於用同樣的方式去看待它。
人們說數字不是真實的,因為你摸不著它們。可是有許多東西是真實的現實但我摸不著,比如饑餓。」
她說:「所以我更願意談論具體、實在的東西,我們可以摸得到、可以直接與之互動的東西;而抽象的事物,我們只能在腦子裏跟它們互動。」
數學是抽象的,但抽象概念也可以無比真實,跟其他真實的事物一樣。

一方面,可以說數學就是現實。比如生物學基於化學,而化學本質上服從物理學定律,這樣我們就自然說到數字和數學了。再想想蔚藍的天空,可以用折射光的波長理論來解釋……那全都是數字。
看來,在更深的層次上,物質的現實具有數學屬性。
但同時數學似乎無法解答人類生活中一些至關重要的事,比如愛情、饑餓和生命。
所以,在所有這些重要的問題中,我們或許可以比較肯定地回答的只有一個,那就是關於數學究竟是表述現實的模型還是現實本身這個問題我們無法找到確切答案。
我們還可以肯定地說,我們找不到那個答案。但如果不去尋找,就得不出這個結論。